Batidos en pendulos acoplados

Pendulos acoplados mediante un resorte

Enunciado

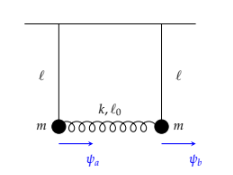
Tenemos dos pendulos identicos acoplados por un resorte cuyos extremos podemos suponer atados a cada masa. Las masas \(m\), las longitudes de las cuerdas \(l\) son iguales. Nuestro trabajo sera encontrar los modos normales y algun movimiento con alguna condición inicial que le impongamos.

Movimiento de las masas

Como digimos, vamos a considerar las masas iguales.

!pip install ffmpeg-python

Requirement already satisfied: ffmpeg-python in c:\users\hp\appdata\local\programs\python\python311\lib\site-packages (0.2.0)
Requirement already satisfied: future in c:\users\hp\appdata\local\programs\python\python311\lib\site-packages (from ffmpeg-python) (1.0.0)

#Importamos algunas librerías útiles
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc # librería de animaciones
rc('animation', html='html5') #para poder ver la animacion en formato inline
from IPython.display import HTML
from PIL import Image  # Pillow se instala como PIL

#Definimos los parámetros del problema
g = 9.81
L = 0.5
m = 1.0 #masas iguales
k = 0.9

Encontremos los modos

Los desplazamientos de las masas seran los angulos \(\psi_a\) y \(\psi_b\). Estos desplazamentos seran pequeños, esto es, si para un pendulo la ecuación de Newton es: \(\ddot{\psi} = \frac{g}{l}.\sin{\psi}\) Si tomamos la función de Taylor del seno a primer orden nos queda que \(\sin{\psi} \sim \psi\) para ángulos pequeños. Apicando esto a las ecuaciones de Newton para nuestro sistema, tenemos:

\[-m.g.\frac{\psi_b}{l}-k(\psi_b-\psi_a)=m.\ddot{\psi}_b\] \[-m.g.\frac{\psi_a}{l}-k(\psi_a-\psi_b)=m.\ddot{\psi}_a\]

Estas ecuaciónes hay que desacoplarlas. Podriamos aplicar el metodo matricial directamente, pero tambien podemos notar lo siguiente. Tomemos los cambios de variable \(\Phi_1 = \psi_b+\psi_a\) y \(\Phi_2=\psi_b-\psi_a\). Jugando un poco con estas ecuaciónes vamos a llegar a las siguientes:

\[\ddot{\Phi}_1 + \frac{g}{l}. \Phi_1 = 0\] \[\ddot{\Phi}_2 \left( \frac{g}{l} + \frac{2.k}{m}\right).\Phi_2 = 0\]

Tenemos dos grados de libertad en el problema, por lo que esperábamos tener dos modos. Uno de ellos se corresponde con no excitar el resorte, por lo que la frecuencia natural coincide con la de un pendulo y el otro al movimiento en contrafase de las masas el cual involucra las interacciones de las masas con las tensiones de los pendulos y el resorte dando lugar a una frecuencia natural que involucra a ambas interacciones.

Frecuencia baja: \(\omega_1 = \sqrt{\frac{g}{l}}\)

Frecuencia alta: \(\omega_1 = \sqrt{\frac{g}{l} + \frac{2.k}{m}}\)

Notar que tenemos dos osciladores armonicos, luego las soluciones para cada una sera:

\[\Phi_1(t) = A_1 .\cos{\left(\sqrt{\frac{g}{l}}.t + \phi_1\right)}\] \[\Phi_2(t) = A_2 .\cos{\left( \sqrt{\frac{g}{l} + \frac{2.k}{m}} . t + \phi_2\right)}\]

Las funciones \(\Phi_1\) y \(\Phi_2\) son las denominadas coordenadas normales, las cuales son las ecuaciónes de movimiento cuando estan desacoplados, luego cuando la oscilación del sistema vibra solo con una de estas ecuaciónes se la denomina Modo normal y equivale al movimiento de todas las particulas involucradas en el sistema con la misma frecuencia (la frecuencia normal caracteristica al modo exitado) y la misma fase inicial.

Simplificando, las posiciónes desacopladas cuando \(A_1=A_2=A\) y \(\phi_1=x\phi_2=0\)

\[\psi_a = \frac{\Phi_1(t) -\Phi_2(t)}{2} = A .\cos{\left(\sqrt{\frac{g}{l}}.t \right)}- A .\cos{\left( \sqrt{\frac{g}{l} + \frac{2.k}{m}} . t\right)}\] \[\psi_b = \frac{\Phi_1(t) +\Phi_2(t)}{2} = A .\cos{\left(\sqrt{\frac{g}{l}}.t \right)}+ A .\cos{\left( \sqrt{\frac{g}{l} + \frac{2.k}{m}} . t\right)}\]

Donde, escrito de forma matricial, podriamos decir lo siguiente:

\[\begin{bmatrix} \psi_a \\ \psi_b \end{bmatrix} = \mathbb{D}.\mathbb{\Phi} = a_1 .\begin{bmatrix} 1 \\ 1 \end{bmatrix}. \cos{\left(\sqrt{\frac{g}{l}}.t + \phi_1 \right)} + a_2 .\begin{bmatrix} 1 \\ -1 \end{bmatrix}. \cos{\left(\sqrt{\frac{g}{l} + \frac{2.k}{m}}.t + \phi_2 \right)}\]

Obteniendo asi:

Modo 1: \(\omega_1 = \sqrt{\frac{g}{L}}\), \(v_1 = \binom{1}{1}\)

Modo 2: \(\omega_2 = \sqrt{\frac{g}{L}+ \frac{2k}{m}}\), \(v_2 = \binom{1}{-1}\)

#Definimos las frecuencias de los modos
#Modo 1: frecuencia más baja
w1 = np.sqrt(g/L) #Es la frecuencia de un péndulo

#Modo 2:
w2 = np.sqrt(g/L+2*k/m) #aparece la información del resorte, es el modo en contrafase

Primero veamos gráficamente cómo es la oscilación cuando estamos en cada uno de los modos.

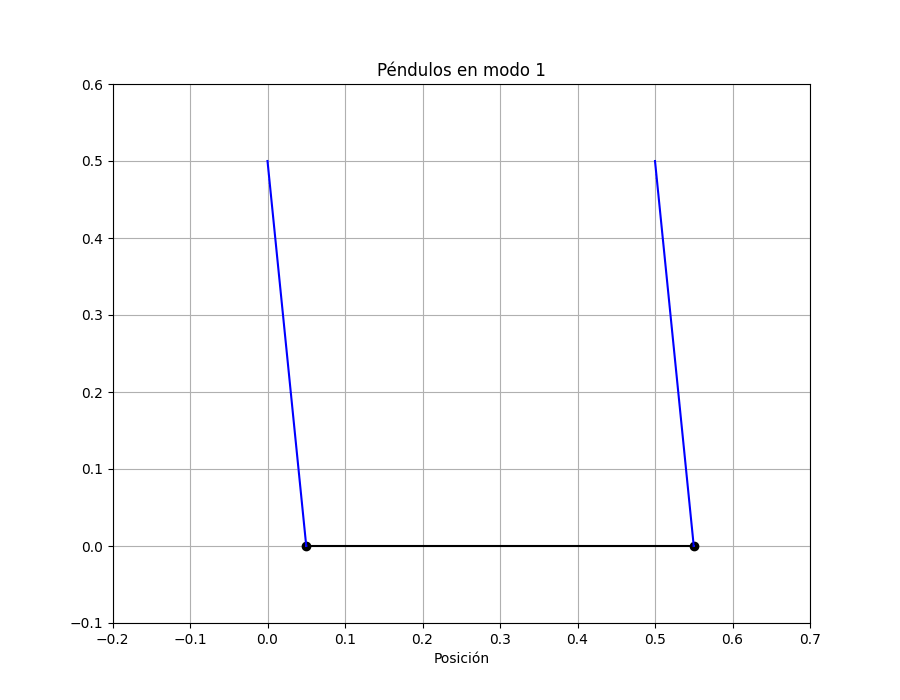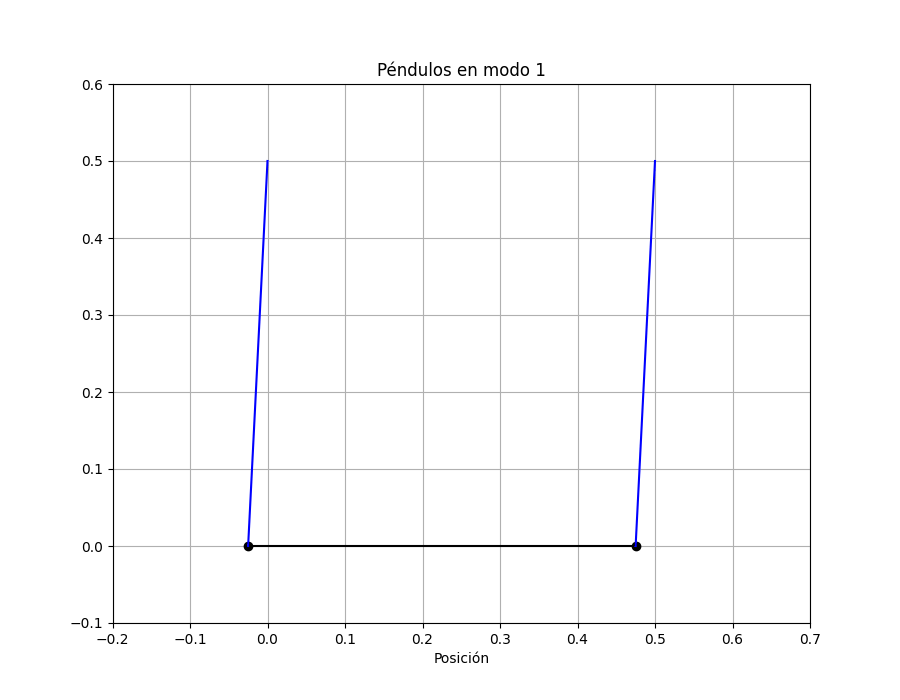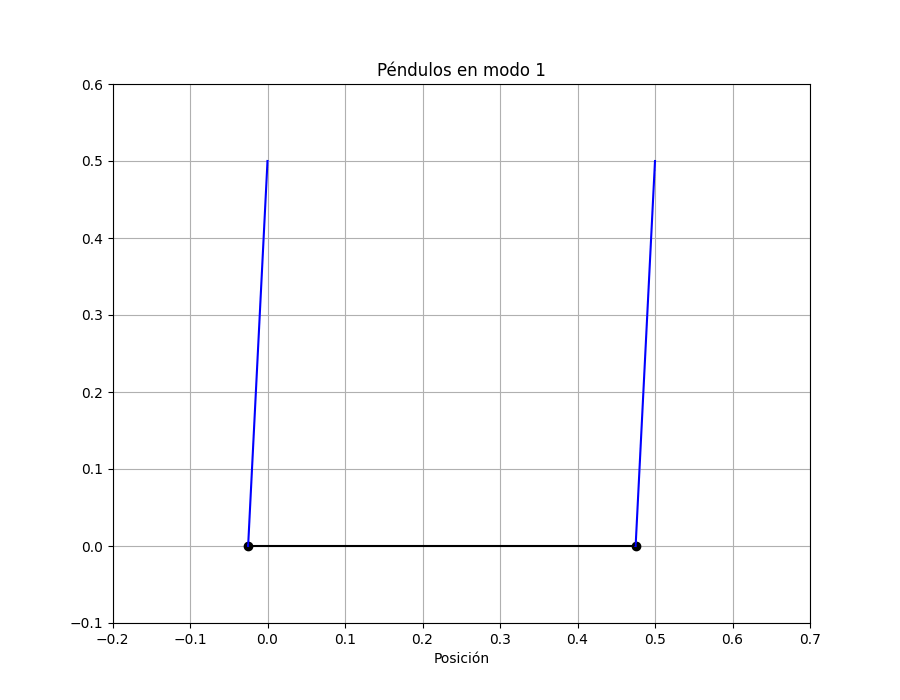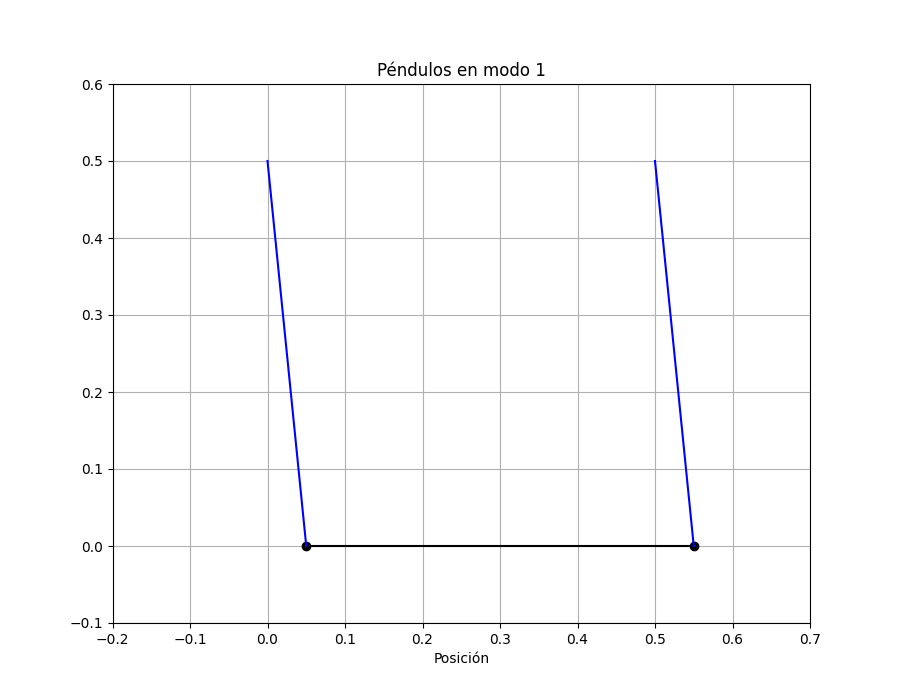
MODO 1:

#Veamos como es la oscilación en el modo 1. Las dos masas están en fase:
t=np.linspace(0,2*np.pi/w1,1000) #defino el vector de tiempos
psi_a1 = 0.05*np.cos(w1*t) #Solución modo 1 para la masa a
psi_b1 = 0.05*np.cos(w1*t) #Solución modo 1 para la masa b

var1=psi_a1 #variable que quiero animar
var2=psi_b1 #variable que quiero animar

fig, ax = plt.subplots(figsize=(9,7));

ax.set_xlim(-0.2,0.7);
ax.set_ylim(-0.1,0.6);
plt.xlabel('Posición');
plt.title('Péndulos en modo 1');

line1, = ax.plot([], [],'ok-');
line2, = ax.plot([], [],'b-');
line3, = ax.plot([], [],'b-');

plt.grid();


def animate(i):
    X = [var1[i],0.5+var2[i]] #lo =0.5
    Y = [0,0]
    line1.set_data(X,Y)
    line2.set_data([0,var1[i]],[0.5,0])
    line3.set_data([0.5,0.5+var2[i]],[L,0])
    return (line1,line2,line3)
  
anim2 = animation.FuncAnimation(fig, animate, frames=len(t), interval=2*np.pi/w1);
#anim2.save('anim_1.gif',writer='pillow')
#HTML(anim2.to_jshtml())

print(type(line1))

<class 'matplotlib.lines.Line2D'>

Vemos que al estar en fase el resorte no se estira ni se comprime, tiene sentido que no aparezca en la frecuencia del modo el k.

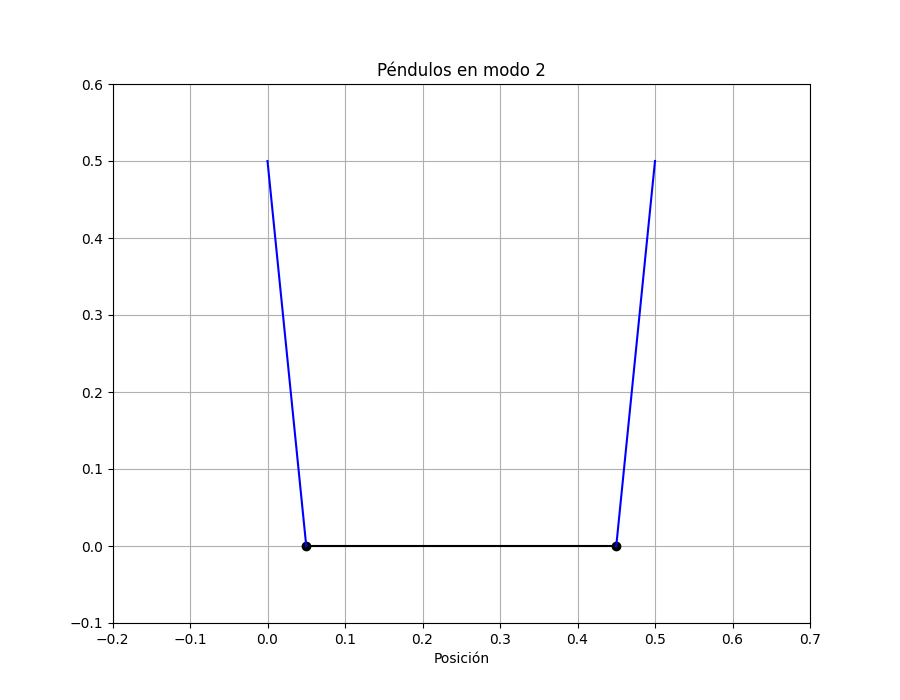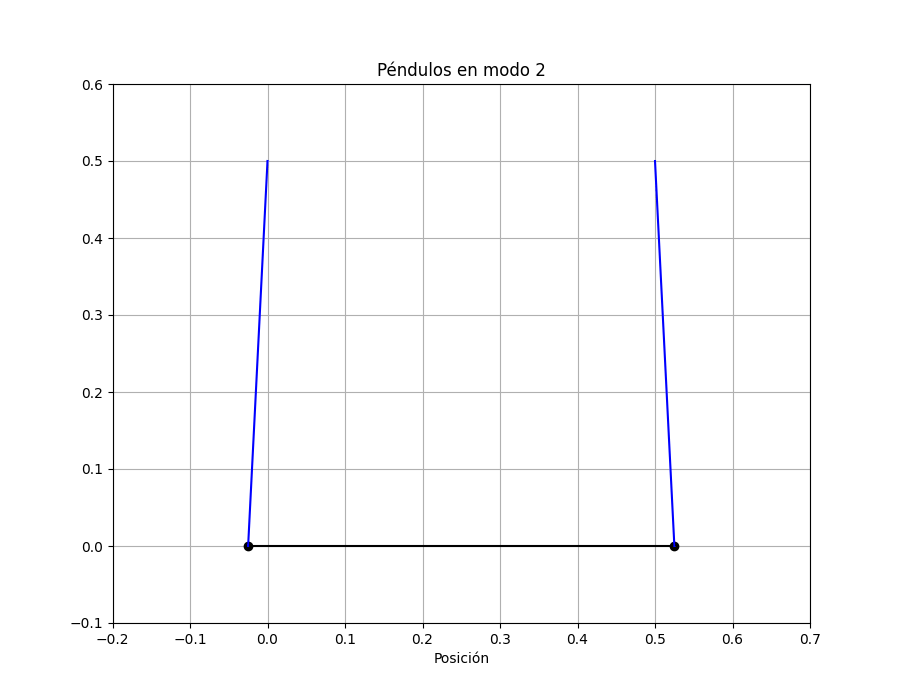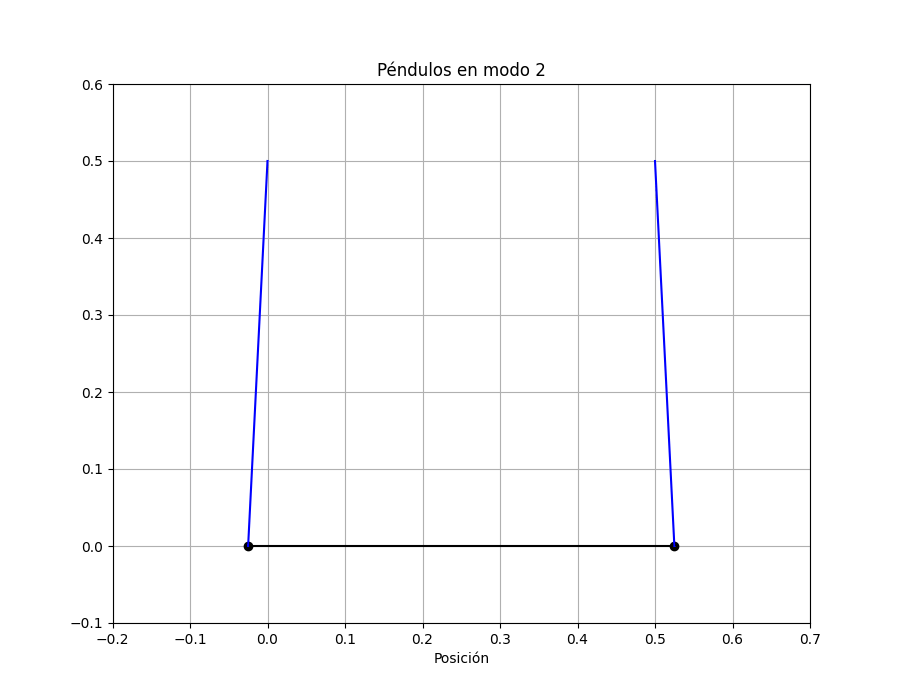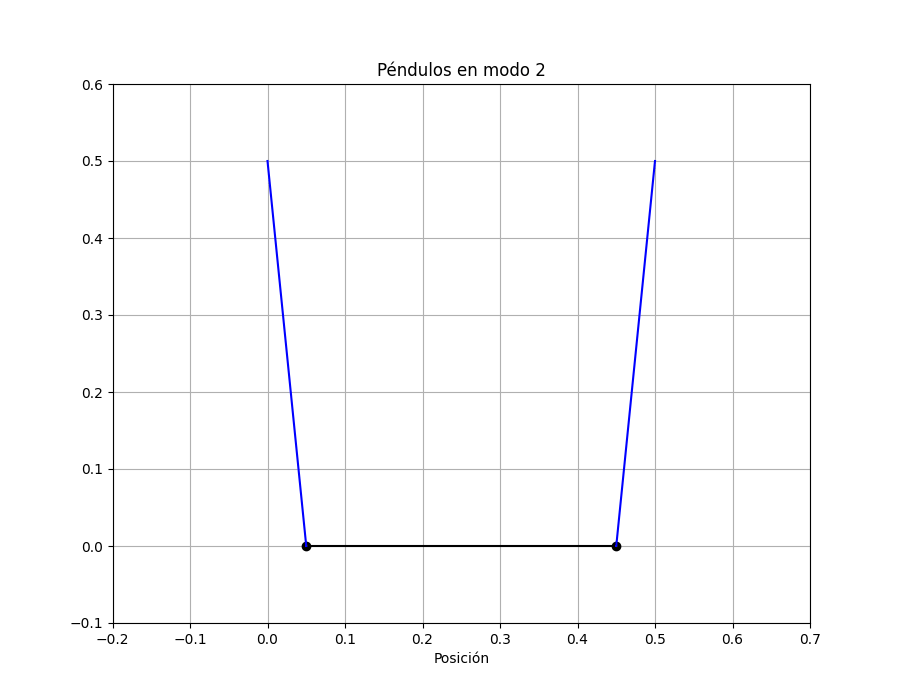
Veamos ahora cómo oscila el sistema en el modo 2:

t=np.linspace(0,2*np.pi/w2,1000) #defino el vector de tiempos
psi_a2 = 0.05*np.cos(w2*t) #Solución modo 2 para la masa a
psi_b2 = -0.05*np.cos(w2*t) #Solución modo 2 para la masa b

var1=psi_a2 #variable que quiero animar
var2=psi_b2 #variable que quiero animar

fig, ax = plt.subplots(figsize=(9,7));

ax.set_xlim(-0.2,0.7);
ax.set_ylim(-0.1,0.6);
plt.xlabel('Posición');
plt.title('Péndulos en modo 2');

line1, = ax.plot([], [],'ok-');
line2, = ax.plot([], [],'b-');
line3, = ax.plot([], [],'b-');

plt.grid();


def animate(i):
    X = [var1[i],0.5+var2[i]]
    Y = [0,0]
    line1.set_data(X,Y)
    line2.set_data([0,var1[i]],[L,0])
    line3.set_data([0.5,0.5+var2[i]],[L,0])
    return (line1,line2,line3)
  
anim2 = animation.FuncAnimation(fig, animate, frames=len(t), interval=2*np.pi/w2);
#anim2.save('anim_2.gif',writer='pillow')
#HTML(anim2.to_jshtml())

Para oscilar en contrafase el resorte tiene que estirarse y comprimirse. Notar que en los dos modos, como esperamos, las dos masas pasan por la posición de equilibrio al mismo tiempo.

Veamos una solución general, que puede escribirse como una combinación lineal de los dos modos. Pueden probar otras combinaciones.

t=np.linspace(0,10,1000) #defino el vector de tiempos
psi_a = 0.05*np.cos(w1*t) + 0.08*np.cos(w2*t) #masa a
psi_b = 0.05*np.cos(w1*t) - 0.08*np.cos(w2*t)  #masa b
plt.plot(t,psi_a, label = "Masa a")
plt.plot(t,psi_b + 0.5, label = "Masa b")
plt.xlabel("Tiempo")
plt.xlabel("Posición x")
plt.legend()
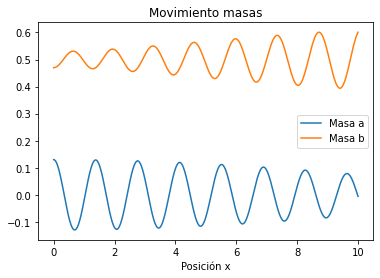
plt.title("Movimiento masas")
plt.show()

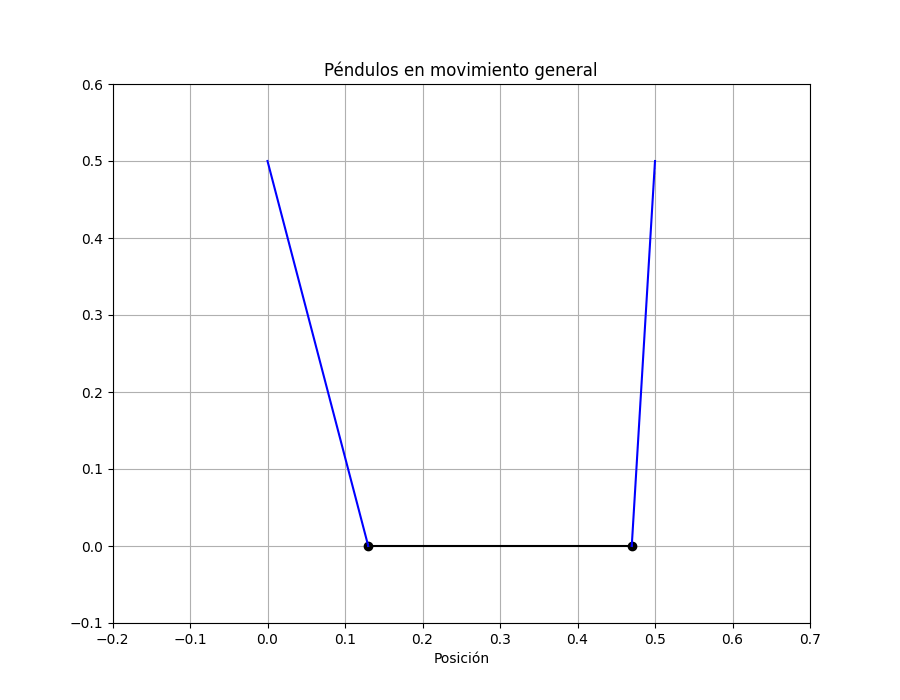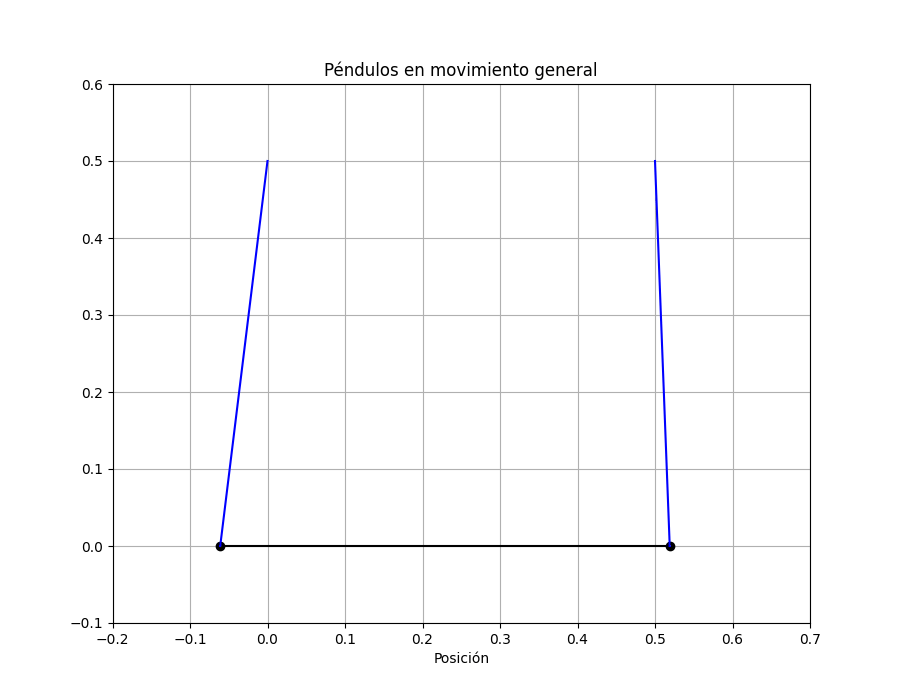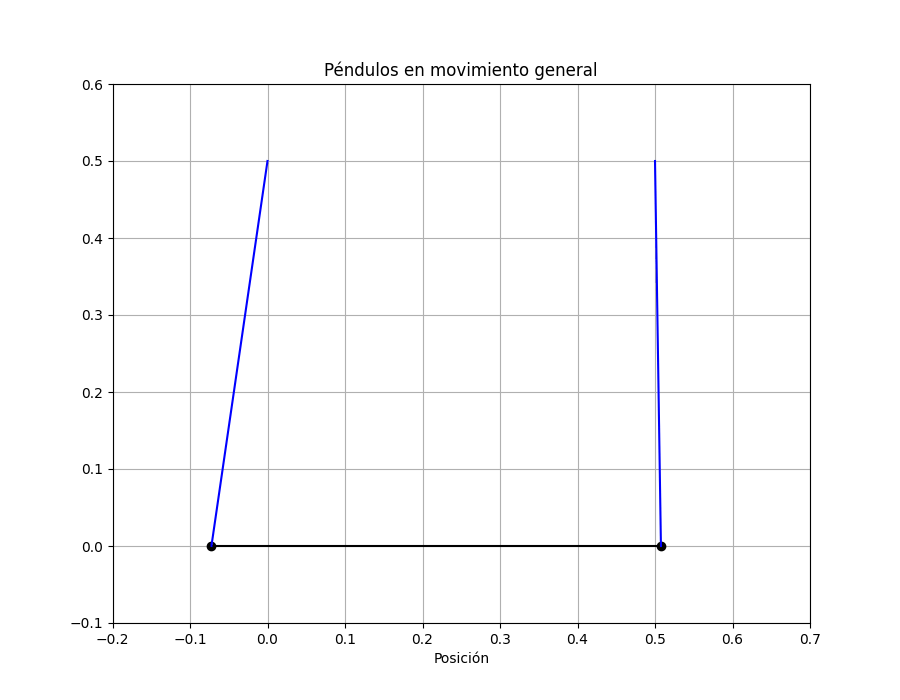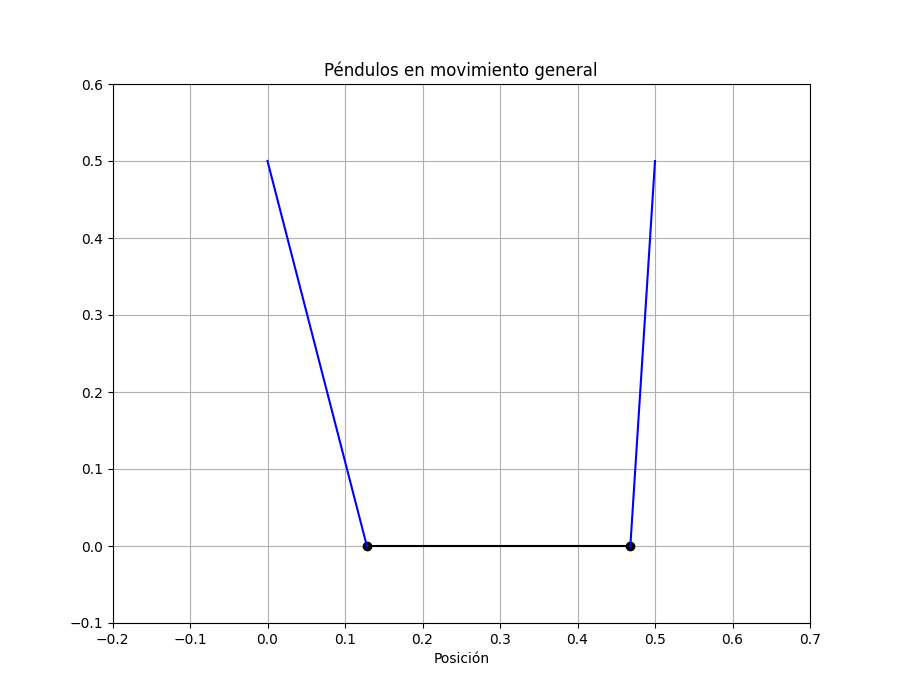
Notar que el movimiento de casa masa no está descrita por un coseno o seno sino por la suma. Veamos cómo es el movimiento de los péndulos.

t=np.linspace(0,2*np.pi/w2,1000) #defino el vector de tiempos
psi_a = 0.05*np.cos(w1*t) + 0.08*np.cos(w2*t) #masa a
psi_b = 0.05*np.cos(w1*t) - 0.08*np.cos(w2*t)  #masa b
var1=psi_a #variable que quiero animar
var2=psi_b #variable que quiero animar

fig, ax = plt.subplots(figsize=(9,7));

ax.set_xlim(-0.2,0.7);
ax.set_ylim(-0.1,0.6);
plt.xlabel('Posición');
plt.title('Péndulos en movimiento general');

line1, = ax.plot([], [],'ok-');
line2, = ax.plot([], [],'b-');
line3, = ax.plot([], [],'b-');

plt.grid();


def animate(i):
    X = [var1[i],0.5+var2[i]]
    Y = [0,0]
    line1.set_data(X,Y)
    line2.set_data([0,var1[i]],[L,0])
    line3.set_data([0.5,0.5+var2[i]],[L,0])
    return (line1,line2,line3)
  
anim2 = animation.FuncAnimation(fig, animate, frames=len(t), interval=2*np.pi/w2);
#anim2.save('anim_3.gif',writer='pillow')
#HTML(anim2.to_jshtml())

Acoplamiento débil: Batidos

Si consideramos el límite de acoplamiento débil, es decir que \(k << \frac{g}{L}\frac{m_a m_b}{m_a +m_b}\), y para el caso de masas iguales, esta condición se resumen en: \(k << \frac{mg }{2L}\), o bien: \(\frac{2k}{m} << \frac{g}{L}\). Esto implica que la frecuencia del modo 2 es similar a la del modo 1.

2*k/m

1.8

g/L

19.62

Notar que el primer término -asociado al resorte- es un orden menor que el segundo -asociado a la frecuencia del péndulo-, por lo que podemos asegurar que, con los parámetros que elegimos al principio, estamos en esta aproximación.

Vamos a ver cómo es la solución teniendo en cuenta esta aproximación y usando que las condiciones de contorno son \(\dot{\psi_a}(0) = 0, \dot{\psi_b}(0) = 0, \psi_a(0)=0,\psi_a(0)=1\). Con estas condiciones podemos escribir las soluciones para las dos masas:

\(\vec{\psi} = A \left[ \binom{1}{1} \cos(\omega_1t) + \binom{1}{-1} \cos(\omega_2 t) \right]\), con A = 1/2.

Para cada masita:

\(\psi_a = A \left[ \cos(\omega_1 t) + cos(\omega_2 t) \right]\) \(\psi_b = A \left[ \cos(\omega_1 t) - cos(\omega_2 t) \right]\)

Si bien ya tenemos bien definido el movimiento de cada masita en el tiempo (y con Python es fácil graficarlo) queremos llegar a una expresión que nos de más idea de cómo es el movimiento.

#Definimos dos frecuencias:
w_p=(w1+w2)/2.0 #promedio de las dos
w_d=(w2-w1)/2.0   #asociada a las diferencias
print("w1:" + str(w1))
print("w2:" + str(w2))
print("Promedio de las frecuencias wp:" + str(w_p))
print("Diferencia de las frecuencias wd:" + str(w_d))

w1:4.4294469180700204
w2:4.628174586162454
Promedio de las frecuencias wp:4.528810752116238
Diferencia de las frecuencias wd:0.09936383404621685

Notar que como habíamos mencionado anteriormente las frecuencias de los dos modos son similares. Por otra parte, las dos frecuencias que definimos difieren en órdenes de magnitud.

t = np.linspace(0,2*np.pi/w_d,1000)
x = np.cos(w_p*t)
y = np.cos(w_d*t)

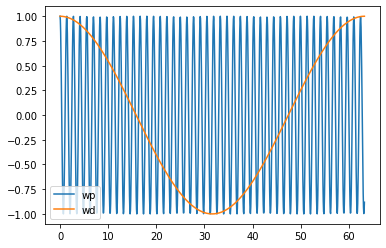
plt.plot(t,x,label="wp")
plt.plot(t,y,label="wd")
plt.legend(loc=3)
plt.show()

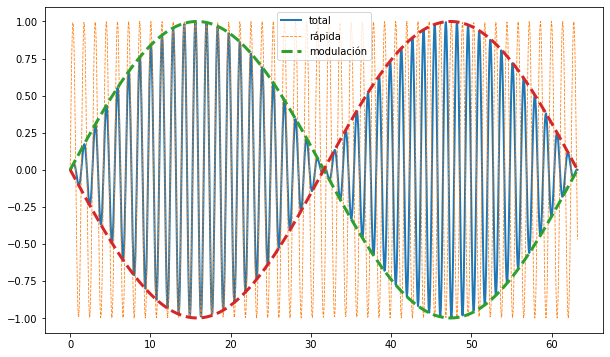
Vemos que hay una frecuencia rápida (\(\omega_p\)) y una lenta (\(\omega_d\)). Vamos a escribir las soluciones para las masitas en términos de estas frecuencias:

t = np.linspace(0,2*np.pi/w_d,1000)
psia = 0.05*np.sin(w_p*t)*np.sin(w_d*t) #masa a
psib = 0.05*np.cos(w_p*t)*np.cos(w_d*t) #masa b

total = np.sin(w_p*t)*np.sin(w_d*t)
oscilacion_rapida = np.sin(w_p*t)
amplitud_modulada = np.sin(w_d*t)
amplitud_modulada2 = -np.sin(w_d*t)
plt.figure(figsize=(10,6))
plt.plot(t,total, linewidth = 2, label="total")
plt.plot(t,oscilacion_rapida, "--", linewidth=0.8, label="rápida")
plt.plot(t,amplitud_modulada,"--", linewidth=3, label="modulación")
plt.plot(t,amplitud_modulada2,"--", linewidth=3)
plt.legend()
plt.show()

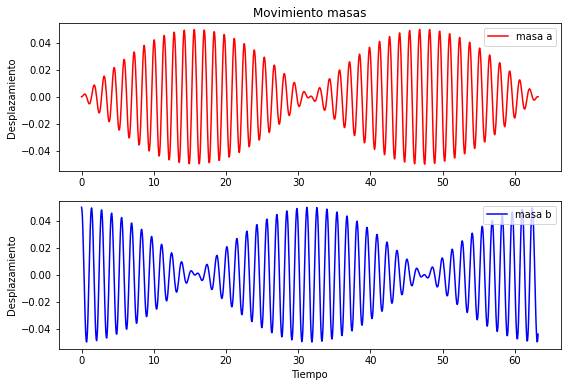
plt.figure(figsize=(9,6))
plt.subplot(211)
plt.plot(t, psia, "r", label="masa a")
plt.ylabel('Desplazamiento')
plt.legend()
plt.title("Movimiento masas")
plt.subplot(212)
plt.plot(t, psib ,"b", label='masa b')
plt.ylabel('Desplazamiento')
plt.legend(loc=1)
plt.xlabel('Tiempo')
plt.show()

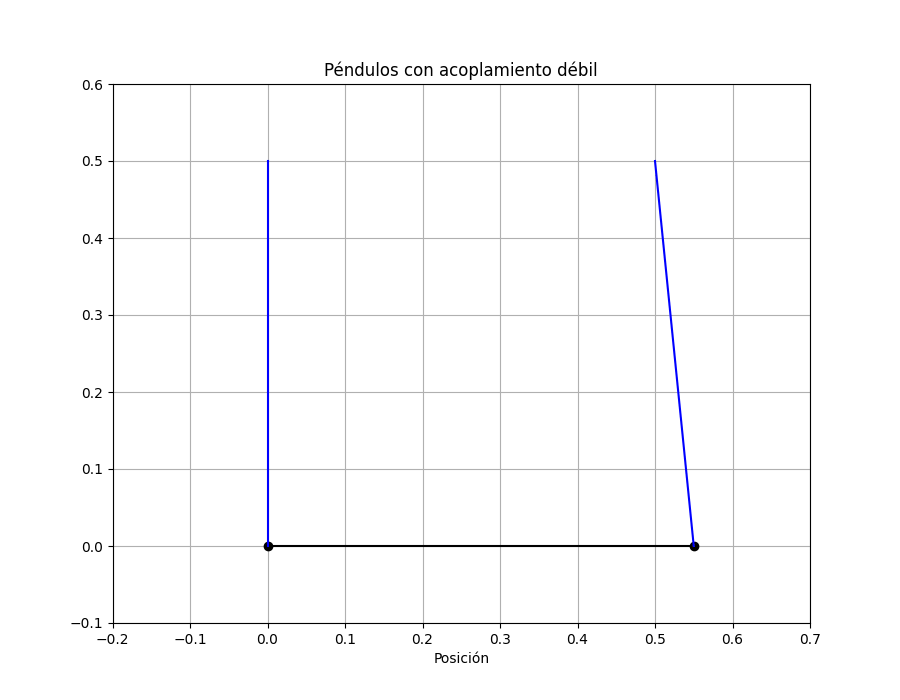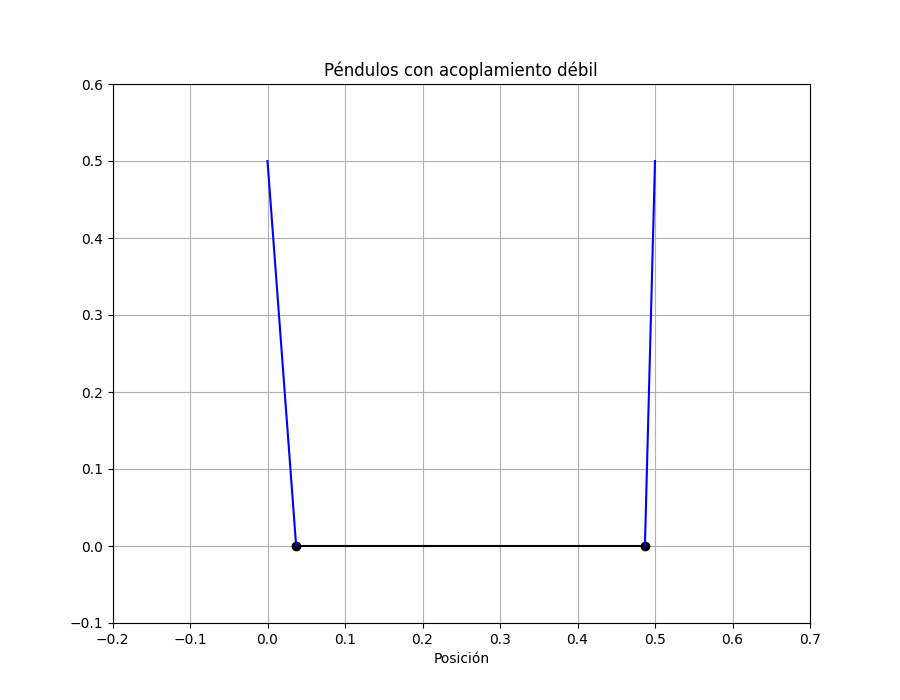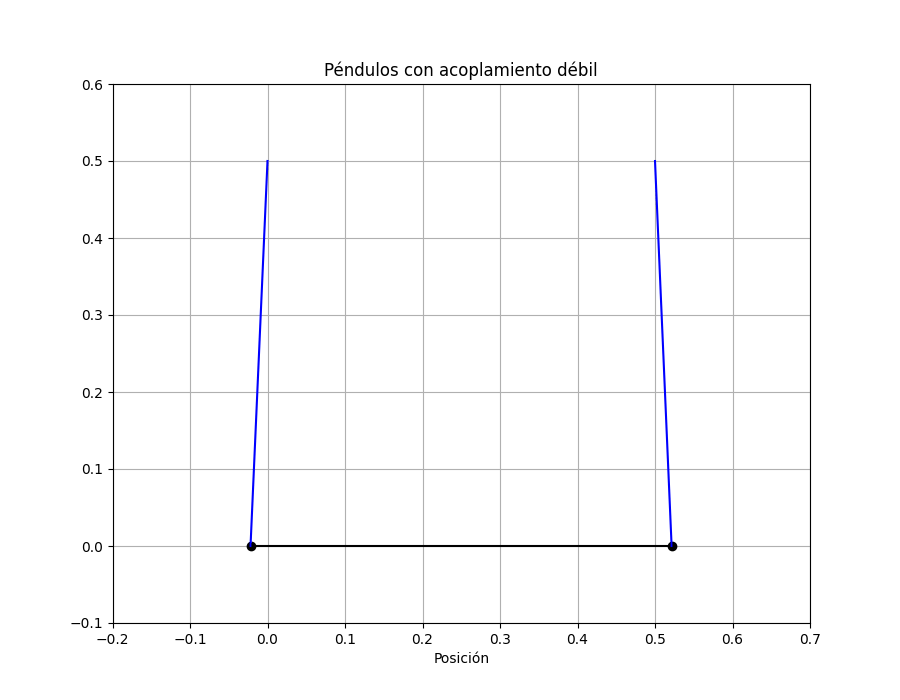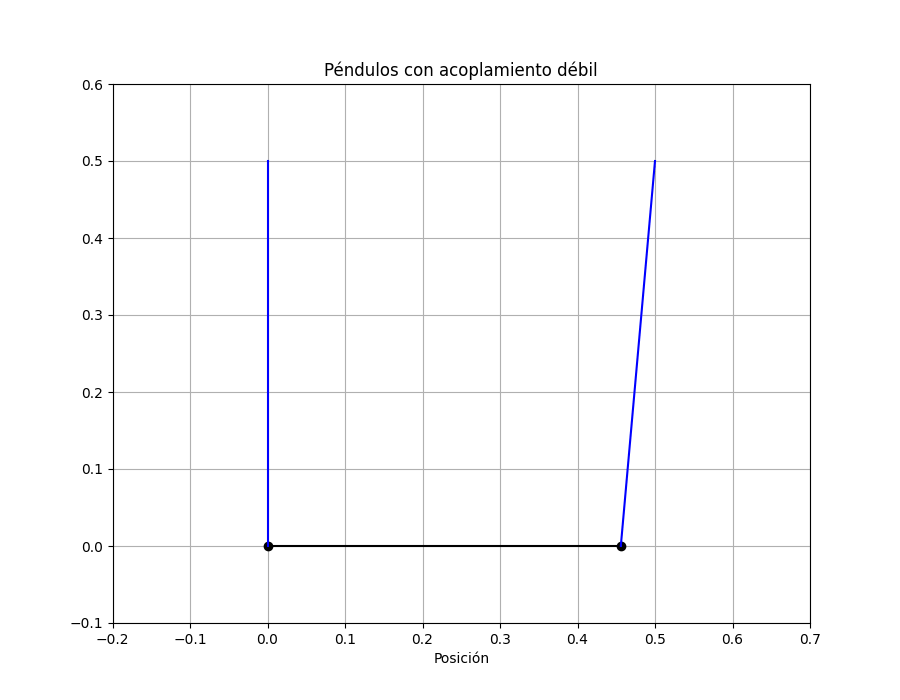
Animación de las masas

Cuando una es máxima la otra está en su mínimo. Veamoslo en la animación del movimiento:

from matplotlib import animation, rc # librería de animaciones
rc('animation', html='html5') #para poder ver la animacion en formato inline
from IPython.display import HTML

var1=psia #variable que quiero animar
var2=psib #variable que quiero animar


fig, ax = plt.subplots(figsize=(9,7));

ax.set_xlim(-0.2,0.7);
ax.set_ylim(-0.1,0.6);
plt.xlabel('Posición');
plt.title('Péndulos con acoplamiento débil');

line1, = ax.plot([], [],'ok-');
line2, = ax.plot([], [],'b-');
line3, = ax.plot([], [],'b-');

plt.grid();


def animate(i):
    X = [var1[i],0.5+var2[i]]
    Y = [0,0]
    line1.set_data(X,Y)
    line2.set_data([0,var1[i]],[L,0])
    line3.set_data([0.5,0.5+var2[i]],[L,0])
    return (line1,line2,line3)
  
anim2 = animation.FuncAnimation(fig, animate, frames=len(t), interval=2*np.pi/w_d);
#anim2.save('anim_4.gif',writer='pillow')
#HTML(anim2.to_jshtml())

Energía

Valores medios en un ciclo rápido de \(T_a\) y \(T_b\) (energía cinética de las masas)

T_a = m*L**2*(0.0025)*(w_p**2-(w_p**2-w_d**2**2)*np.cos(w_d*t)**2)
T_b = m*L**2*(0.0025)*(w_p**2-(w_p**2-w_d**2**2)*np.sin(w_d*t)**2)

plt.figure(figsize=(9,6))
plt.subplot(211)
plt.plot(t, T_a,"r",label="a")
plt.ylabel('Energía cinética media')
plt.legend()
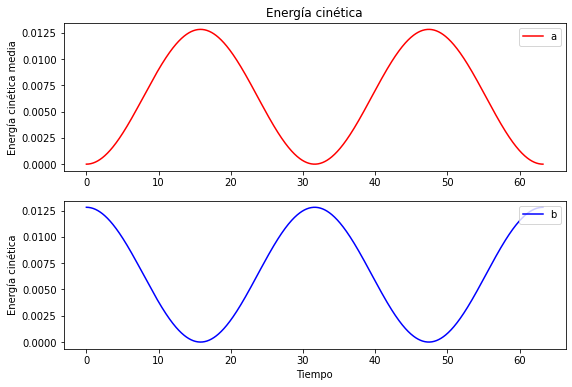
plt.title("Energía cinética")
plt.subplot(212)
plt.plot(t, T_b ,"b", label='b')
plt.ylabel('Energía cinética')
plt.legend(loc=1)
plt.xlabel('Tiempo')
plt.show()

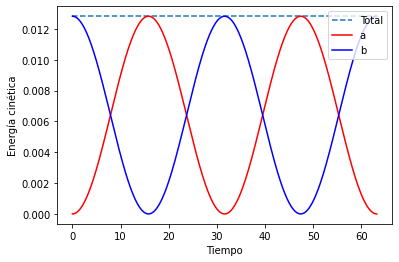
Vemos que la energía cinética media (promediando sobre las oscilaciones rápidas) oscila. Vemos que cuando es máxima para una masa, es mínima para la otra: tenemos una transferencia de la energía cinética.

plt.plot(t, T_a+T_b, "--", label = "Total")
plt.plot(t, T_a,"r",label="a")
plt.plot(t, T_b ,"b", label='b')
plt.ylabel('Energía cinética')
plt.legend(loc=1)
plt.xlabel('Tiempo')
plt.show()