Distribución cuadrada de cargas discretas sobre carga de prueba en el centro

Enunciado del Problema

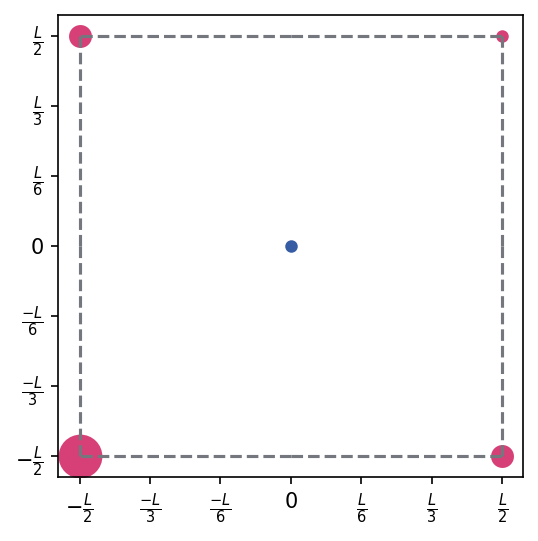
Hallar la fuerza neta sobre una carga q ubicada en el centro de un cuadrado de lado L, cuando se han colocado cargas q, 2q, 4q y 2q, en los cuatro vértices (en ese orden). Para simplificar el cálculo, tenga en cuenta la simetría de la configuración de cargas.

# @title Librerias necesarias
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
import scipy.constants as cte
import matplotlib.gridspec as gridspec
from matplotlib import animation, rc
from IPython.display import HTML
from numba import njit
rc('animation', html='jshtml')

# @title Definición de constantes

ε_0 = cte.epsilon_0
π = cte.pi
ke = 1/(4*π*ε_0) # [ke] = N.m^2/kg^2
G = 6.7e-11 # [G] = N m^2/kg^2

#@title Grafica del Problema. (No es la unica Configuración posible)
#@title { display-mode: "form" }

# Datos
L = 10 # m
d = L/np.sqrt(2)  # m
q = 1e-4 # C
r = np.array([0, 0])
ord = np.linspace(0,1,L)

# Distribución espacial de las cargas
coords = np.array([(d, d), (-d, d), (-d, -d), (d, -d)])
cargas = np.array([q, 2*q, 4*q, 2*q])

# Calculo de la fuerza electrica
F = []
def Coulomb(q1, r1, q2, r2):
    r12 = r1 - r2
    F = q1*q2*(r12/(np.linalg.norm(r12)**3))/(4*cte.pi*cte.epsilon_0)
    return F

for r2, q2 in zip(coords, cargas):
    F.append(Coulomb(q,r,q2,r2))

# Ploteo de las cargas y los vectores
plt.figure(figsize=(4, 4), dpi=150)

# Carga central. q
plt.plot(r[0],r[1],color="#365DA3", marker='o',markersize=q*5e+4)

# Cargas en los vertices. Observar el orden de las coordenadas
for i in range(4):
    plt.plot(coords[i-1,0],coords[i-1,1],color="#D64076", marker='o',markersize=cargas[i-1]*5e+4)

# Dibujo un cuadrado ficticio
#Cada tupla representa la mitad de un lado del cuadrado. Observar el orden
cuadrado = np.array([(ord*0+d, ord*d), (ord*0+d, -ord*d),
                    (ord*0-d, ord*d), (ord*0-d, -ord*d),
                    (ord*d, ord*0+d), (ord*(-d), ord*0+d),
                    (ord*d, ord*0-d), (ord*(-d), ord*0-d)])
for i in range(8):
  plt.plot(cuadrado[i-1,0], cuadrado[i-1,1], color="#74787E", linestyle='--')

marcas_grafico = [r'$-\frac{L}{2}$', r'$\frac{-L}{3}$', r'$\frac{-L}{6}$', '$0$', r'$\frac{L}{6}$', r'$\frac{L}{3}$', r'$\frac{L}{2}$']

plt.yticks(np.arange(-d, (4/3)*d, d/3), marcas_grafico)
plt.xticks(np.arange(-d, (4/3)*d, d/3), marcas_grafico)
plt.show()

Aplicando la superposición

Este ejercicio es un ejercicio simple en el cual debemos aplicar el concepto de superposición. Esto es, que dada una carga de prueba $q$ esta interactua con las otras cargas distribuidas de alguna forma en el espacio y como resultado se ve que la fuerza total que siente dicha carga viene dada por la sumatoria de las fuerzas individuales de las cargas presentes en la distribución. Matematicamente: \(\vec{F}_{total}=q \sum_{i=1}^{n} \vec{E}_i = q \sum_{i=1}^{n} q_i k_e \frac{\vec{r}-\vec{r}_i}{\Vert\vec{r}-\vec{r}_i\Vert^3}\) Ahora solo queda entender cuales son los vectores posición de cada carga de la distibución. En este caso, la carga de prueba esta ubicada en el centro y las de la distribución en cada vertice del cuadrado.

1. $q_1=2q$ ubicada en $\vec{r}_1 = (-L/2,L/2)$
2. $q_2=q$ ubicada en $\vec{r}_2 = (L/2, L/2)$
3. $q_3=2q$ ubicada en $\vec{r}_3 = (L/2,-L/2)$
4. $q_4=4q$ ubicada en $\vec{r}_4 = (-L/2,-L/2)$

En particular, analizando la simetria del sistema podemos darnos cuenta que las fuerzas de las cargas $q_1$ y $q_3$ son de igual modulo y opuestas, no por el signo, sino por su posición. Luego, la carga de prueba $q$

Ahora, el calculo de la norma $\Vert\vec{r}-\vec{r}_i\Vert$ va a dar el mismo valor para cada posición de las cargas, ya que la carga de prueba esta ubicada justo en el centro del cuadrado. Entonces, calculemos solo una vez esta norma: \(\Vert\vec{r}-\vec{r}_i\Vert = \sqrt{(x-x_i)^2 + (y-y_i)^2} =\) \(\sqrt{\left(\frac{L}{2}\right)^2 + \left(\frac{L}{2}\right)^2} = \frac{\sqrt{2}L}{2}\)

• Calculamos $\vec{F}_{total}$: \(\vec{F}_{total}=q \sum_{i=1}^{n} \vec{E}_i =\) \(=\frac{q.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(q_1.\left((0,0)-(-\frac{L}{2},\frac{L}{2})\right) + q_2.\left((0,0)-(\frac{L}{2},\frac{L}{2})\right) + q_3.\left((0,0)-(\frac{L}{2},-\frac{L}{2})\right) + q_4.\left((0,0)-(-\frac{L}{2},-\frac{L}{2})\right)\right)=\) \(=\frac{q.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(q_1.\left((\frac{L}{2},-\frac{L}{2})\right) + q_2.\left((-\frac{L}{2},-\frac{L}{2})\right) + q_3.\left((-\frac{L}{2},\frac{L}{2})\right) + q_4.\left((\frac{L}{2},\frac{L}{2})\right)\right)=\) \(=\frac{q.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(2q.\left((\frac{L}{2},-\frac{L}{2})\right) + q.\left((-\frac{L}{2},-\frac{L}{2})\right) + 2q.\left((-\frac{L}{2},\frac{L}{2})\right) + 4q.\left((\frac{L}{2},\frac{L}{2})\right)\right)=\)

\(=\frac{q.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(\left(2q.\frac{L}{2},-2q.\frac{L}{2}\right) + \left(-q.\frac{L}{2},-q.\frac{L}{2}\right) + \left(-2q.\frac{L}{2},2q.\frac{L}{2}\right) + \left(4q.\frac{L}{2},4q.\frac{L}{2}\right)\right)=\) \(=\frac{q.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(2q.\frac{L}{2}-q.\frac{L}{2}-2q.\frac{L}{2}+4q.\frac{L}{2},-2q.\frac{L}{2}-q.\frac{L}{2}+2q.\frac{L}{2}+4q.\frac{L}{2}\right) =\) \(=\frac{3q^2.k_e}{(\frac{\sqrt{2}L}{2})^3}. \left(\frac{L}{2},\frac{L}{2}\right)\) Notemos que nos que las fuerzas de las cargas $q_1$ y $q_3$ se anulan por simetria, luego la superposición se podria haber obtenido solo haciendo la cuenta con las cargas $q_2$ y $q_4$.

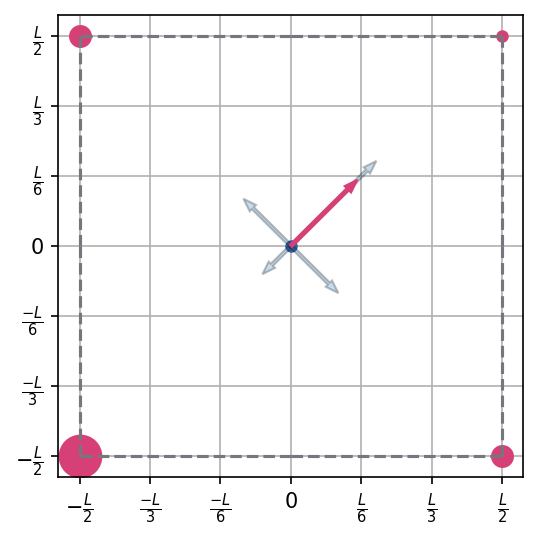
#@title Fuerzas de cada particula y resultante en rosa
# Ploteo de las cargas y los vectores
plt.figure(figsize=(4, 4), dpi=150)

# Carga central. q
plt.plot(r[0],r[1],color="#365DA3", marker='o',markersize=q*5e+4)

# Cargas en los vertices. Observar el orden de las coordenadas
for i in range(4):
    plt.plot(coords[i-1,0],coords[i-1,1],color="#D64076", marker='o',markersize=cargas[i-1]*5e+4)

# Dibujo un cuadrado ficticio
#Cada tupla representa la mitad de un lado del cuadrado. Observar el orden
cuadrado = np.array([(ord*0+d, ord*d), (ord*0+d, -ord*d),
                    (ord*0-d, ord*d), (ord*0-d, -ord*d),
                    (ord*d, ord*0+d), (ord*(-d), ord*0+d),
                    (ord*d, ord*0-d), (ord*(-d), ord*0-d)])
for i in range(8):
  plt.plot(cuadrado[i-1,0], cuadrado[i-1,1], color="#74787E", linestyle='--')

# Así dibujo las flechas
for x, y in F:
    plt.arrow(r[0], r[1], x, y, width=0.1, zorder=10, alpha=0.25)
# Esta es la resultante
plt.arrow(r[0], r[1], *sum(F), color="#D64076", width=0.1, zorder=11)
plt.grid()


marcas_grafico = [r'$-\frac{L}{2}$', r'$\frac{-L}{3}$', r'$\frac{-L}{6}$', '$0$', r'$\frac{L}{6}$', r'$\frac{L}{3}$', r'$\frac{L}{2}$']

plt.yticks(np.arange(-d, (4/3)*d, d/3), marcas_grafico)
plt.xticks(np.arange(-d, (4/3)*d, d/3), marcas_grafico)
plt.show()

Intentemos dibujar el campo

Ahora, habiendo descubierto cual es la fuerza resultante, estaria bueno poder visualizar que esta pasando con el campo de toda la distribución.

Implementemos esto en python

# @title Defino una función para calcular el campo electrico
def E(xp, yp, xf=0, yf=0, q=1):
    """Campo Eléctrico en 2 Dimensiones
    en un punto de prueba xp, yp
    de una carga fuente en un punto xf, yf
    de valor q
    """

    Dx = xp - xf
    Dy = yp - yf

    den = (Dx**2 + Dy**2)**1.5

    # Noten que la respuesta e sun vector (Ex, Ey).
    return q * Dx / den, q * Dy / den

# Distribución espacial de las cargas
#coords = np.array([(d, d), (-d, d), (-d, -d), (d, -d)])
#cargas = np.array([q, 2*q, 4*q, 2*q])

# @title Campo eléctrico en 2 Dimensiones
def E2(xp, yp):
    """Campo Eléctrico en 2 Dimensiones
    en un punto de prueba xp, yp
    de dos cargas separadas una distancia a sobre el eje y
    de valor q1 y q2
    """

    # Calculo el campo de cada carga ...
    E1x, E1y = E(xp, yp, coords[0][0], coords[0][1], cargas[0])
    E2x, E2y = E(xp, yp, coords[1][0], coords[1][1], cargas[1])
    E3x, E3y = E(xp, yp, coords[2][0], coords[2][1], cargas[2])
    E4x, E4y = E(xp, yp, coords[3][0], coords[3][1], cargas[3])

    # y sumo porque vale superposicion.
    return E1x + E2x + E3x + E4x, E1y + E2y + E3y + E4y

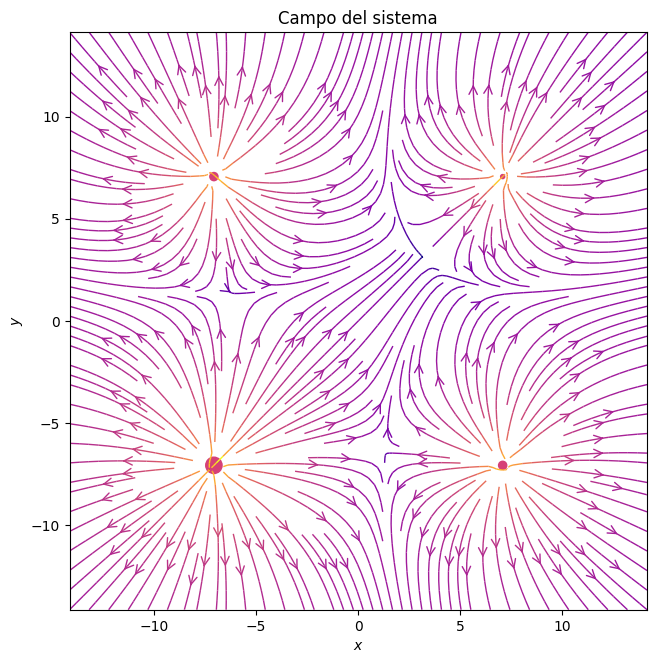
# @title Ploteo
# Generamos una grilla donde vamos a calcular el campo eléctrico
nx, ny = 60, 60
rangoX = np.linspace(-d*2, d*2, nx)*1
rangoY = np.linspace(-d*2, d*2, ny)*1
grillaX, grillaY = np.meshgrid(rangoX, rangoY)

# Y calculamos los campos para la grilla definida
Ex, Ey = E2(grillaX, grillaY)


fig = plt.figure(figsize=(7.5,7.5))
ax = fig.add_subplot(111)


color = np.log(np.sqrt(Ex**2 + Ey**2))
ax.streamplot(grillaX, grillaY, Ex, Ey, color=color, linewidth=1, cmap=plt.cm.plasma,
              density=2, arrowstyle='->', arrowsize=1.5)

#ax.add_artist(Circle([0,0], 0.1, color="#4CE7D2"))

ax.add_artist(Circle([coords[0][0],coords[0][1]], 0.1, color="#D64076"))
ax.add_artist(Circle([coords[1][0],coords[1][1]], 0.2, color="#D64076"))
ax.add_artist(Circle([coords[2][0],coords[2][1]], 0.4, color="#D64076"))
ax.add_artist(Circle([coords[3][0],coords[3][1]], 0.2, color="#D64076"))

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_xlim(-d*2,d*2)
ax.set_ylim(-d*2,d*2)
ax.set_aspect('equal')
ax.set_title('Campo del sistema')
plt.show()

En este grafico podemos visualizar que esta pasando y confirmar lo que le sucede a la carga puntual. No hay que olvidar que estamos en un modelo electrostatico, por lo que no estamos viendo que sucede a lo largo del tiempo.